Lazy Merkle Raffle

2023-04-16 • @kevincharm

Preliminaries

• Hash function
• Merkle tree
• Bijectivity
• Feistel cipher

Introduction

This article proposes a novel method of raffling (i.e. picking an arbitrary number of winners from an arbitrarily large list of participants) that is optimised for on-chain environments where storage and compute is expensive, by deferring the computation of winning indices until they are needed. This method applies the pull-over-push pattern that is commonly employed in airdrops, where recipients must claim their airdrop share rather than receiving it directly in their wallets.

Using this new method of raffling, for a raffle picking $n$ winners from some arbitrarily large list of participants, a winner must claim her winning ticket using a Merkle proof $\pi = \langle i, p_i, Q \rangle$ where $i$ is the leaf index of the winner and $Q$ is the ordered set of sibling hashes in the path needed to reconstruct the Merkle root. The index $i$ is then bijectively mapped to a shuffled index $f(i,s)$ using a cycle-walking Feistel cipher $f$ and a committed secure random seed $s$. The win is then valid iff $f(i) < n$.

Merkle Trees for Proving Inclusion and Index

Merkle trees are magical data structures that can be used to compress arbitrarily large lists into a single hash (also known as the Merkle root). This property makes them useful for verifying the integrity of large data sets.

Merkle proofs are used to succinctly prove that an item belongs to an arbitrarily large list by constructing a path from the item to the Merkle root. However, what is not commonly known is that Merkle proofs can also prove the index of that item in the list, given the correct proof format.

Preparing the Merkle tree

To prepare a list of participants for a raffle, we first construct a Merkle tree $M$ of depth $d_M = \lceil\log_2{|L|}\rceil$ using the raffle participants $p_i \in L$ as the leaves, filling the remaining empty leaves with a zero value $0$. Leaf indices should correspond to their positional index $i$ in the original participants list $L$. Figure 2 illustrates how the participants list from Figure 1 should be constructed as a Merkle tree.

index	participant
0	a
1	b
2	c

Figure 1. Example list of raffle participants with their corresponding indices

Figure 2. Merkle tree constructed from raffle participants in Figure 1, with the 2nd leaf c selected, and its accompanying siblings required for the proof of inclusion displayed in purple.

Generating the Merkle proof

With the Merkle tree constructed, it is then possible to generate Merkle proofs to prove the inclusion and the index of each leaf. Figure 3 shows the components of the Merkle proof of the 2nd leaf c derived from the Merkle tree in Figure 2.

Definition: Merkle proof

For a leaf $p_i$ in a Merkle tree $M$ of depth $d_M$, a root $u_M$, and a collision-resistant cryptographic hash function $h(a,b)$, a prover constructs a Merkle proof $\pi = \langle i, p_i, Q \rangle$, where $Q = \{ q_0, q_1, ..., q_{d-1} \}$ denotes the consecutive sibling nodes required as inputs to $h$ on each level, with the corresponding bit of $i$ determining the order of inputs to $h$, to reconstruct $u$ that convinces a verifier that $p_i$ is the $i^{\text{th}}$ leaf of $M$.

Figure 3. The elements comprising a complete Merkle proof in the correct format: the index, leaf, and accompanying siblings.

Lazy Shuffling

At the core of any raffling algorithm is the shuffle that produces an unpredictable permutation of the list of participants. The problem with array-based shuffling algorithms, such as the Fisher-Yates algorithm, is that they require stateful computation to produce the final list of winners. On the EVM, this requires writing multiple times to storage, which makes the algorithm economically expensive. Therefore, there is a need to use a different class of shuffling algorithms - we will refer to this class of algorithms as stateless shuffles.

Definition: Stateless Shuffle

Given a finite ordered set with $k$ elements $X = \{ x_0, x_1, ..., x_{k-1} \}$, and a random seed $s$, a stateless shuffle function $f(x,s)$ maps $X \rightarrow X$ with a permutation $\sigma_{s}$.

It is important that these stateless shuffle algorithms strictly produce permutations of the set of participants in order to enforce the property that raffle winners are drawn without repetition. Figure 4 gives an example of how applying a stateless shuffle function to each element in a finite set $X$ produces a bijective mapping $X \rightarrow X$.

Figure 4. Example of how an instance of a Feistel cipher function bijectively maps a finite domain to a pseudorandom permutation.

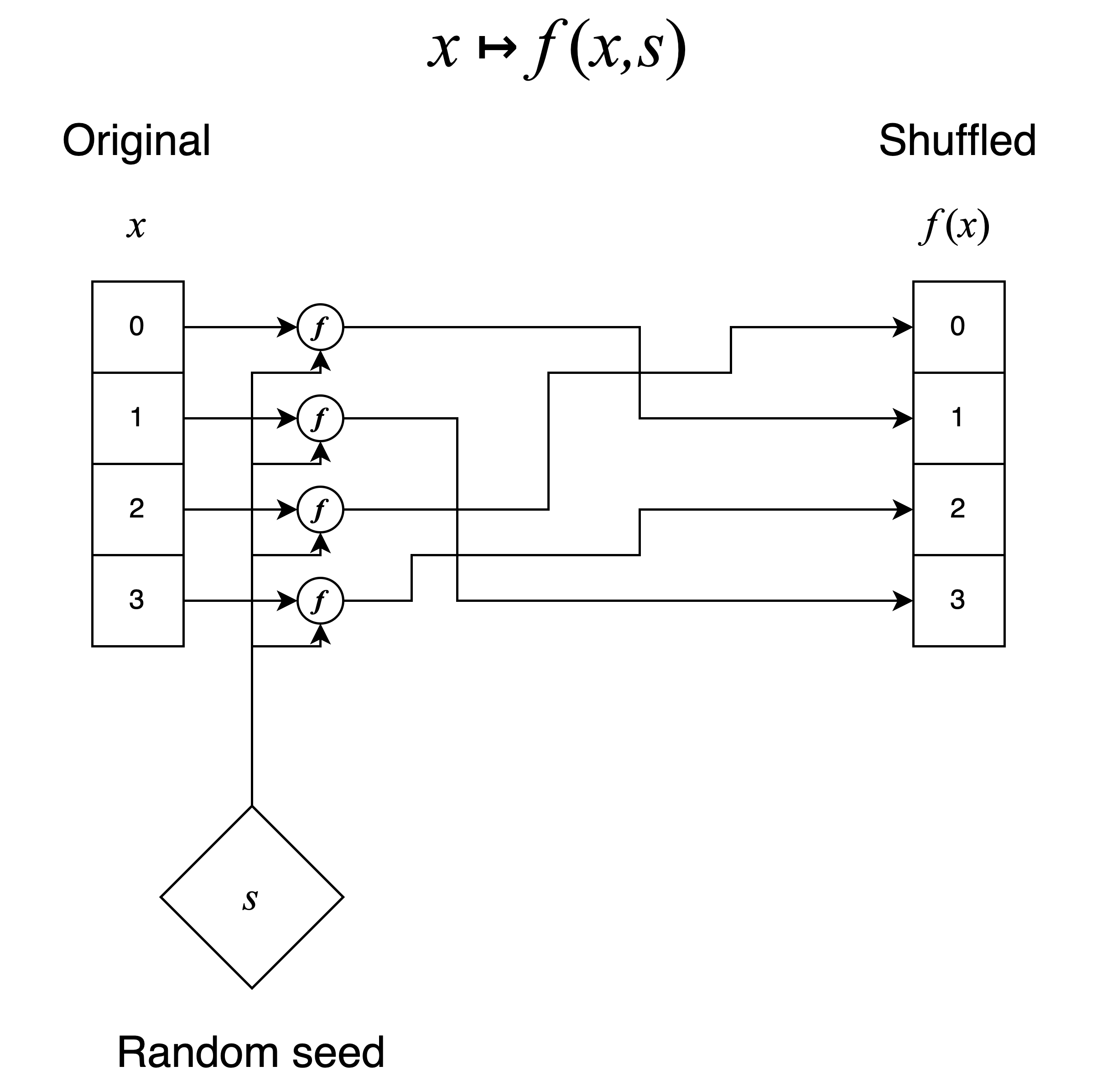
There exists an algorithm to deterministically (based on a given seed) compute a bijective mapping of an index to its shuffled index. In fact, there are at least 2 known algorithms: The Swap-or-not Shuffle and the Feistel Shuffle. Specifically, we use the Feistel Shuffle with rounds set to 4 as it is the most economical of the stateless shuffling algorithms when implemented for the EVM. Of course, an unpredictable secure random seed is still required as an input to these shuffling algorithms.

The Feistel Shuffle

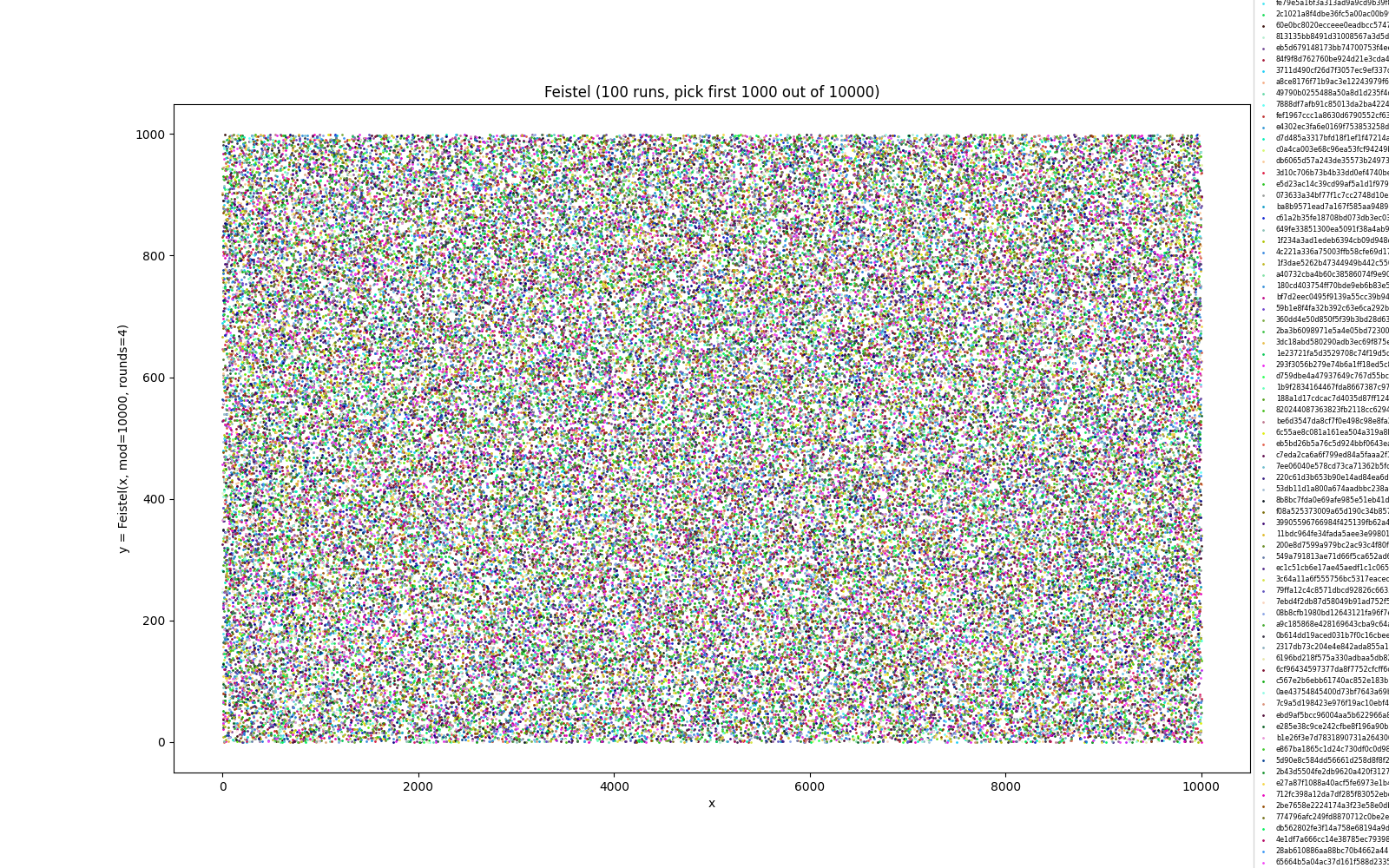
The Feistel Shuffle can cheaply be implemented in the EVM, coming in at ~4350 gas to calculate a permutation for a single index for a list size of 10,000. Feistel ciphers are based on round functions, and these are run a fixed number of times, as specified in the rounds parameter. It is sufficient to set rounds = 4 to make a strong pseudorandom permutation, given a cryptographically secure random seed is used (discussed in this paper by Luby & Rackoff). The Feistel Shuffle was a candidate for computing validator committees in Ethereum Proof-of-Stake consensus specifications with the desired properties of having a distribution being provably close to uniform; and the ability to compute a shuffled index in $\mathcal{O}(1)$.

An example of the distribution of the outputs of a correctly-configured Feistel Shuffle function is shown in Figure 5.

Figure 5. Original index (x-axis) plotted against its shuffled index (y-axis) after being fed through a Feistel shuffle. Each colour is a separate raffle of 1000 winners out of 10000 participants with a unique 32-byte random seed. All runs use 4 rounds of Feistel.

Verifying Winners Just-In-Time

As discussed previously, the winners of a raffle are defined as those participants whose shuffled indices are less than the number of winners to be picked.

Definition: Set of Winners

Given a raffle picking $n$ winners with an ordered set of $k$ participants $P = \{ p_0, p_1, ..., p_{k-1} \}$, and a committed random seed $s$, the ordered set of winners is $W = \{ p_i \mid f(i,s) < n \}$.

While it is possible to eagerly map a stateless shuffle function $f$ over the entire set of participants, we can defer this computation to the moment when raffle participants check whether they've won or not. Upon checking whether an entry is indeed a winning entry, a participant first generates a Merkle proof that proves both the inclusion and the index $i$ of the entry in the original participants list. This index $i$ is then applied as an input to the stateless function $y = f(i,s)$ along with the committed random seed $s$. If the number of winners to pick in the raffle is $n$, then the participant holds a winning entry iff $y < n$.

Most importantly, this verification can be efficiently performed just-in-time inside a smart contract while a participant attempts to claim a prize. The gas overhead of this verification operation on the EVM is equivalent to verification of a Merkle proof plus a few thousand gas for performing a Feistel shuffle.